Les notions de dérivée et de différentielle forment un aspect essentiel des mathématiques, parce qu’elles correspondent à la rencontre des mathématiques en tant que calcul séparé de la physique avec l’évolution dialectique de la réalité elle-même.
Les notions de dérivée et de différentielle relèvent d’un nexus entre mathématiques et physique ; c’est le point où les mathématiques ne peuvent plus se contenter d’être des mathématiques, devenant physique, et où la physique devient mathématique.
C’est la raison pour laquelle Karl Marx a accordé une importance substantielle à la dérivée, la différentielle, voyant en cette dernière l’expression de la négation de la négation ; non seulement il s’exerçait au calcul d’une dérivée et d’une différentielle pour se reposer l’esprit, mais il a laissé un millier de pages de manuscrits mathématiques, dont les plus importantes concernent précisément la dérivée et la différentielle.
Pour comprendre adéquatement cette question, il faut bien saisir que tout se joue au niveau d’une variable, c’est-à-dire d’un nombre qui se voit être modifié. La réflexion à ce sujet est directement dans le prolongement de l’association de l’algèbre à la géométrie.
On se rappellera ici de ce qu’a dit la savante française Sophie Germain (1776-1831) :
« L’algèbre n’est qu’une géométrie écrite, la géométrie n’est qu’une algèbre figurée. »

Friedrich Engels, dans La dialectique de la Nature, nous dit à ce sujet que :
« La grandeur variable de Descartes a marqué un tournant en mathématique.
C’est avec elle que le mouvement et la dialectique sont entrés dans la mathématique et que devinrent tout de suite indispensables le calcul différentiel et intégral ; qui naissent d’ailleurs immédiatement et devaient être en général et dans l’ensemble mis au point, non pas inventés, par Newton et Leibniz ».
Il y a cependant un problème de fond qui va se poser ; pour cela il faut comprendre comment on procède à une dérivée et à une différentielle.
Imaginons que nous suivions le parcours d’un cycliste pendant une dizaine de secondes.
Le déplacement se fait à 20 km/h de manière régulière, soit environ 5,5 mètres par seconde. Voici le nombre de mètres parcourus par seconde, pendant les dix secondes.
| 1 | 5,56 |
| 2 | 11,12 |
| 3 | 16,68 |
| 4 | 22,24 |
| 5 | 27,80 |
| 6 | 33,36 |
| 7 | 38,92 |
| 8 | 44,48 |
| 9 | 50,04 |
| 10 | 55,60 |
Il est également possible de retracer ces dix secondes sur un graphique, au moyen d’un repère cartésien.
Sur la ligne horizontale, on a les secondes, sur la ligne verticale, le nombre de mètres parcourus ; autrement dit, la ligne horizontale représente le temps, la ligne verticale la distance parcourue, c’est-à-dire l’espace.
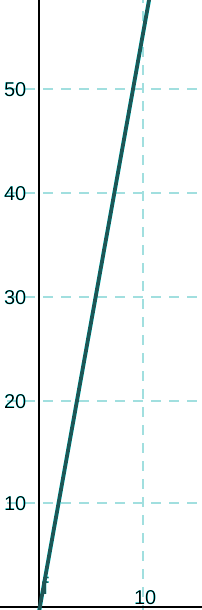
On remarquera que, de manière logique, si l’on divise le nombre de mètres par le temps effectué, on retombe sur 5,56 ; on a ainsi 44,48 : 8 = 5,56, 50,04 : 8 = 5,56, etc.
Autrement dit, l’évolution de y divisé par l’évolution de x permet de retrouver la vitesse : 5,56 mètres par seconde, soit 20 km/h.
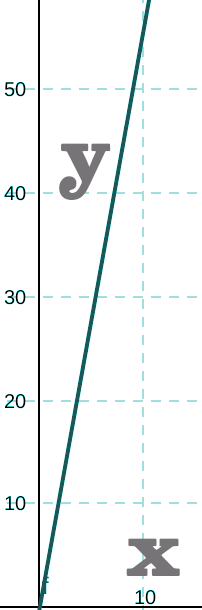
De manière dialectique, si l’on divise les secondes par les mètres effectués, on a également un résultat.
Ainsi, si on prend 8 secondes et 44,48 mètres et qu’on fait 8 : 44,48, on obtient alors 0,179856115.
Cela veut dire qu’on parcourt un mètre en 0,179856115 seconde.
Cela est ici toutefois secondaire, même s’il y a une réflexion fondamentale à faire à ce niveau.
Imaginons maintenant qu’on n’ait pas affaire à un mouvement qui ait une vitesse constante.
Le cycliste, par exemple, commence à accélérer à un moment donné.
On ne peut plus représenter cela par une ligne droite : on obtient une courbe.

La ligne droite connaît une rupture : il y a ici un saut qualitatif dans l’accumulation quantitative.
Dit plus simplement, la vitesse modifiée, ce qui est une qualité, modifie l’accumulation des mètres effectuée par le cycliste, ce qui est une quantité.
Sur un repère cartésien, on voit qu’au début, chaque seconde correspond à peu de mouvement, puis à un moment donné chaque seconde correspond à un mouvement bien plus prononcé.
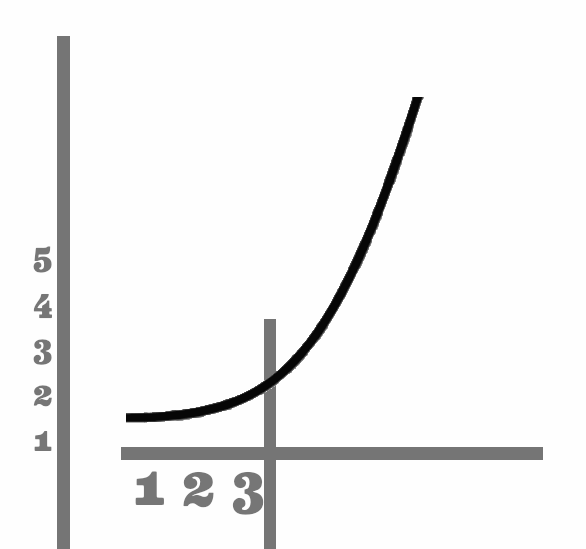
Cela pose un problème pour calculer la vitesse, qui n’est pas la même à chaque moment.
On peut contourner le problème en prenant la vitesse en général, c’est-à-dire en se tournant vers le tout début du mouvement et sa toute fin, pour calculer une moyenne générale.
Si on sait que le cycliste part au temps 0 et parcourt 250 mètres en une minute, on a 250 : 60 = 4,166666667, soit 4,166666667 mètres par seconde, ce qui fait un tout petit plus que 15 km/h.
Cependant, cela ne permet pas de savoir quelle est la vitesse entre deux moments précis – ce qui est le principe de la dérivée – ni quelle est la vitesse à un moment précis – ce qui est le principe de la différentielle.
La méthode employée en mathématiques pour contourner le problème posé par la courbe est le suivant.
On place une ligne droite sur la courbe, de manière la plus correspondante possible à un moment particulier de la courbe nous intéressant spécifiquement.
Cette ligne droite est appelée la tangente, du verbe latin tangere, toucher.

On obtient alors une zone bien particulière, qui va permettre de saisir l’évolution de la courbe pour une partie précise – de manière contournée, puisqu’on va regarder non plus la courbe ou une partie de la courbe en tant que telle, mais la partie de la ligne droite qu’on a plaquée et qui est censée équivaloir grosso modo à la courbe.
Ce grosso modo va jouer un rôle capital par la suite.

Concrètement, voici ce que cela donne.
On a une courbe et dessus on a x’ et y’, extrémités de la partie de la tangente qui nous intéresse.
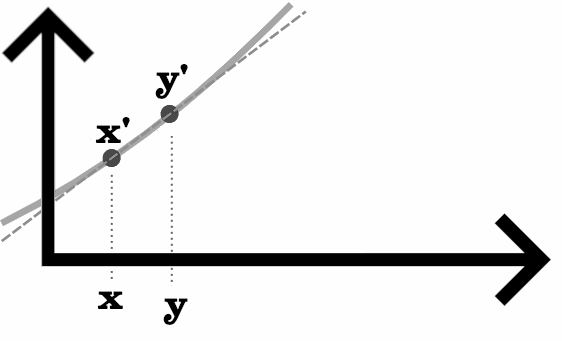
Voici comment on procède.
On remarque qu’il existe une différence entre x et y, puisque ce ne sont pas les mêmes valeurs.
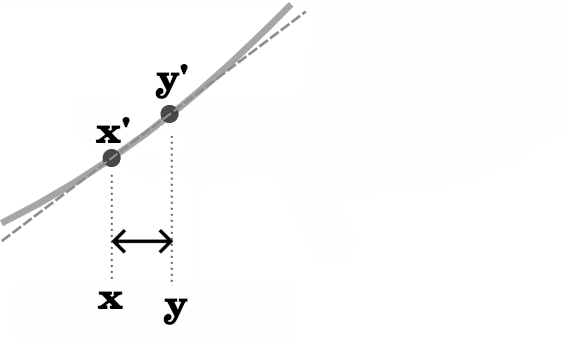
On remarque qu’il y a, par définition, également une différence entre x’ et y’.
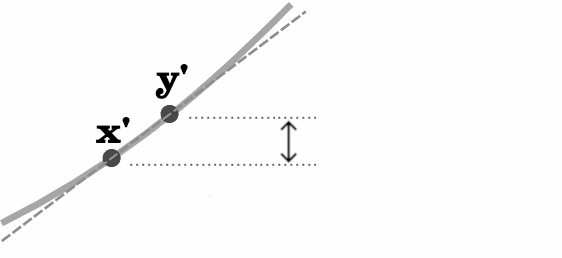
Ces deux différences vont être justement utilisées. Appelons les A et B.
Pour la ligne droite pour faire la moyenne, on avait y divisé par x.

Ici, on divise B par A. Cela veut dire que, dans les faits, on place un repère cartésien au sein d’un repère cartésien, même si ce n’est pas dit ainsi.
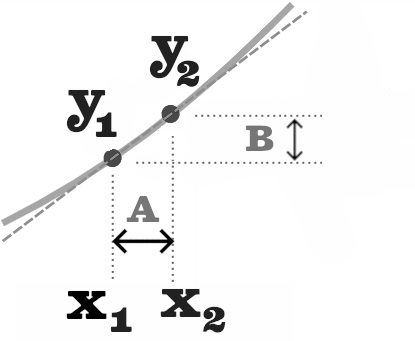
Il ne faut pas oublier que les mathématiques procèdent par association permanente de leurs outils, sans forcément un recul.
Cela va particulièrement se remarquer à un moment dans la différentielle.
On notera ici la remarque intéressante de Jean-Jacques Rousseau dans Les Confessions :
« Je n’ai jamais été assez loin pour bien sentir l’application de l’algèbre à la géométrie.
Je n’aimais point cette manière d’opérer sans savoir ce qu’on fait, et il me semblait que résoudre un problème de géométrie par les équations, c’était jouer un air en tournant une manivelle.
La première fois que je trouvais par le calcul que le carré d’un binôme était composé du carré de chacune de ses parties et du double produit de l’une par l’autre, malgré la justesse de ma multiplication, je n’en voulus rien croire jusqu’à ce que j’eusse fait la figure.
Ce n’était pas que je n’eusse un grand goût pour l’algèbre en n’y considérant que la quantité abstraite ; mais appliquée à l’étendue, je voulais voir l’opération sur les lignes, autrement je n’y comprenais plus rien. »
Concrètement, cela donne la chose suivante avec x, y, x’, y’. On a x qui correspond à x’, y à y’, et inversement, c’est-à-dire que les x indiquent par exemple le temps, les y la distance correspondante, et inversement.
On a ici affaire à une fonction : pour x donné, on a un x’ donné, soit F(x) = x’, F(y) = y’, etc.
Chaque élément, et c’est fondamental ici, dépend dans le repère soit de la ligne horizontale, soit de la ligne verticale (on a l’abscisse comme coordonnée horizontale et l’ordonnée comme coordonnée verticale).

Si on regarde bien A et B, on s’aperçoit des choses suivantes.
On voit que pour passer de x à y, sur la ligne horizontale, on ajoute A. Cela veut dire que x + A = y.
On voit que pour passer de x’ à y’ en se focalisant sur la ligne verticale, on ajoute B. Cela veut dire que x’ + B = y’.
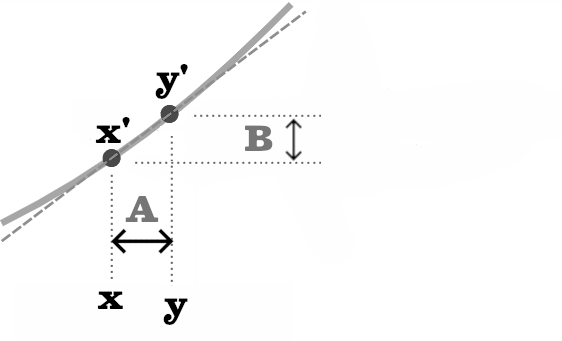
Or, si x + A = y, cela veut dire qu’on peut remplacer y par x + A, et ainsi on peut dire que F(y) = y’ a comme strict équivalent F(x + A) = y’.
Par conséquent, comme x’ + B = y’ et comme F(x + A) = y’, alors x’ + B = F(x + A).
On prend alors F(x) = x’, ce qui fait que :
x’ + B = F(x + A)
On procède alors à un renversement, déplaçant x’ de la gauche vers la droite, en en inversant le sens:
B = F(x + A) – x’
On a alors :
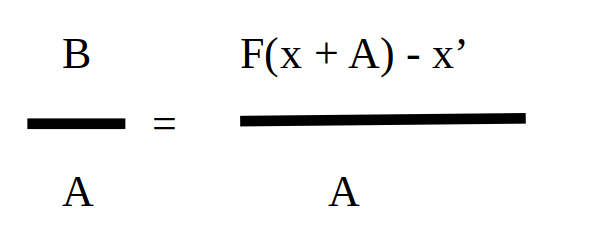
Et comme F(x) = x’, alors :

On a alors un résultat qui présente l’évolution de la contradiction entre x et y et entre x’ et y’, autrement dit dans quelle mesure il y a accélération, davantage d’eau qui coule, plus de sable d’ajouté, etc.
C’est ce qu’on appelle en mathématiques effectuer une dérivée.
Cela présuppose naturellement qu’on connaisse x, y, x’, y’. Il va également de soi que pour qu’un calcul soit le plus juste possible, il faut que l’espace entre x et y soit le plus restreint possible, car n’oublions pas qu’on se rapproche de la courbe au moyen d’une droite : plus cette droite « correspond » à la courbe, plus le résultat sera proche de la réalité.
Regardons maintenant en quoi il y a ici une intense question dialectique, en se tournant vers Karl Marx.
Ce dernier parle de cette question de la dérivée, mais également de celle de la différentielle, les deux choses étant similaires et en même temps fondamentalement différentes, formant une opposition dialectique.
Une dérivée s’appuie sur l’existence de deux points ; sans ces deux points, il n’est pas possible d’effectuer l’opération qu’est la dérivation.
La différentielle est l’équivalent d’une dérivée, mais avec une technique particulière pour ne s’intéresser qu’à un seul point en particulier.
Le problème est alors en effet qu’on ne dispose plus de moyen de faire B/A, puisque pour obtenir A et B, il fallait avoir deux points. Si on a seulement x et F(x) = x’, on n’a pas y et F(y) = y’, et par conséquent on ne dispose plus de A et B.

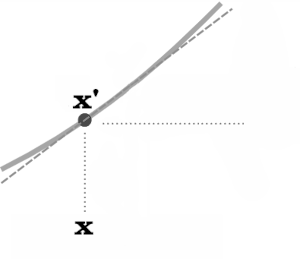
Les mathématiques utilisent alors, afin de passer de la dérivée à la différentielle, la notion de limite.
Autrement dit, on va utiliser un y qui se rapproche le plus possible de x, sans être x pour autant, tout en étant x en même temps.
Une limite va dans les faits être un y virtuel, qu’on va faire tendre le maximum vers x, en reprenant pour cette opération visant la différentielle les principes de la dérivée ; le résultat qu’on cherche est toujours B/A, qu’on va trouver réellement au moyen d’un y virtuel. Il y a là un paradoxe.
Pour les mathématiques, c’est juste un contournement, un y qu’on va mettre entre parenthèses au final, et ce qu’on va mettre de côté est considéré insignifiant du point de vue du calcul.
Pour Karl Marx, justement, il va y avoir ici un point absolument fondamental.
Voyons comment cela se passe.
Le « truc » consiste dans la différentielle en le remplacement de B par Δy et celui de A par Δx. C’est purement symbolique, cela permet d’effacer pour ainsi dire B et A.
On a alors :
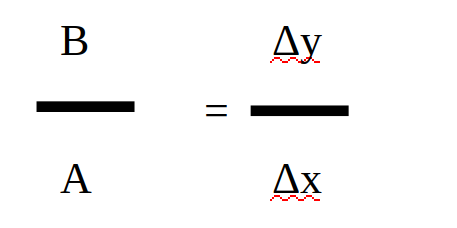
Par conséquent on n’a plus :
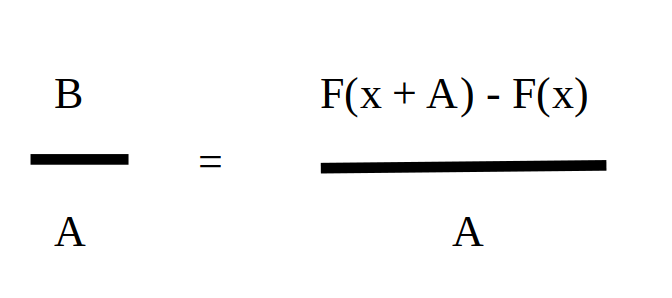
On a désormais :
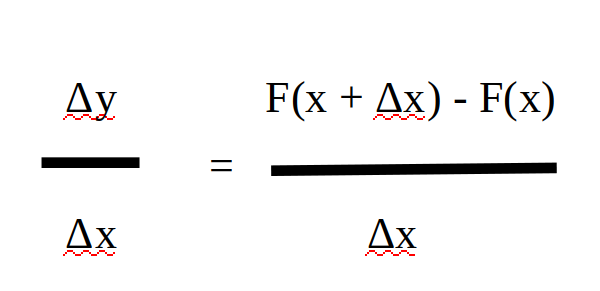
Or, dans ce cas précis, on veut que l’écart entre x et x’ soit le plus restreint possible.
On va donc partir du principe que l’écart est nul, équivalent à 0.
Cela signifie que A, ici Δx, est égal à zéro, car il n’y a aucun « écart » entre x et x’.
Que signifie dans les faits que Δx = 0 ? Eh bien qu’on a :
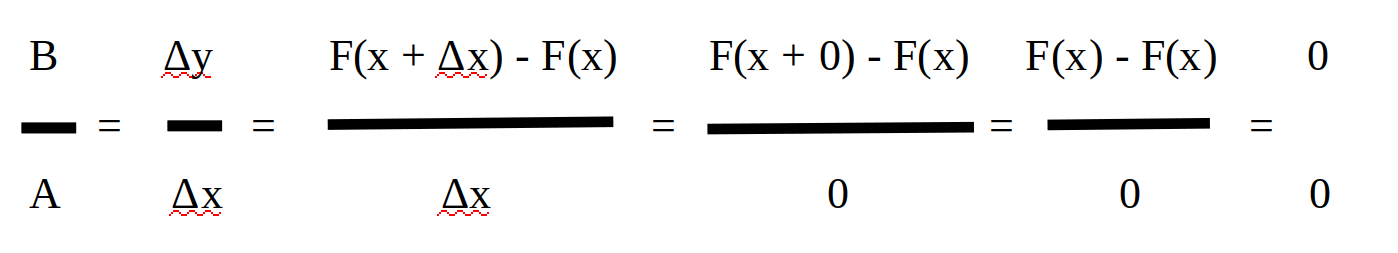
On obtient ici quelque chose dont on ne peut pas se servir mathématiquement.
Et pourtant, cela va servir quand même. Il y a ici un « mystère » qui n’a pas échappé à Karl Marx. Il dit :
« Introduire tout d’abord la différenciation et ensuite la faire disparaître de nouveau ne mène ainsi littéralement à rien.
Toute la difficulté pour comprendre l’opération différentielle (tout comme de toutes façons dans la négation de la négation) tient justement à voir comment elle se distingue d’une telle simple procédure et conduit par là à des résultats réels. »
Voyons comment le processus aboutit dans les faits à un résultat malgré tout.
Prenons la fonction F(x) = x², et prenons le calcul pour obtenir la différentielle.
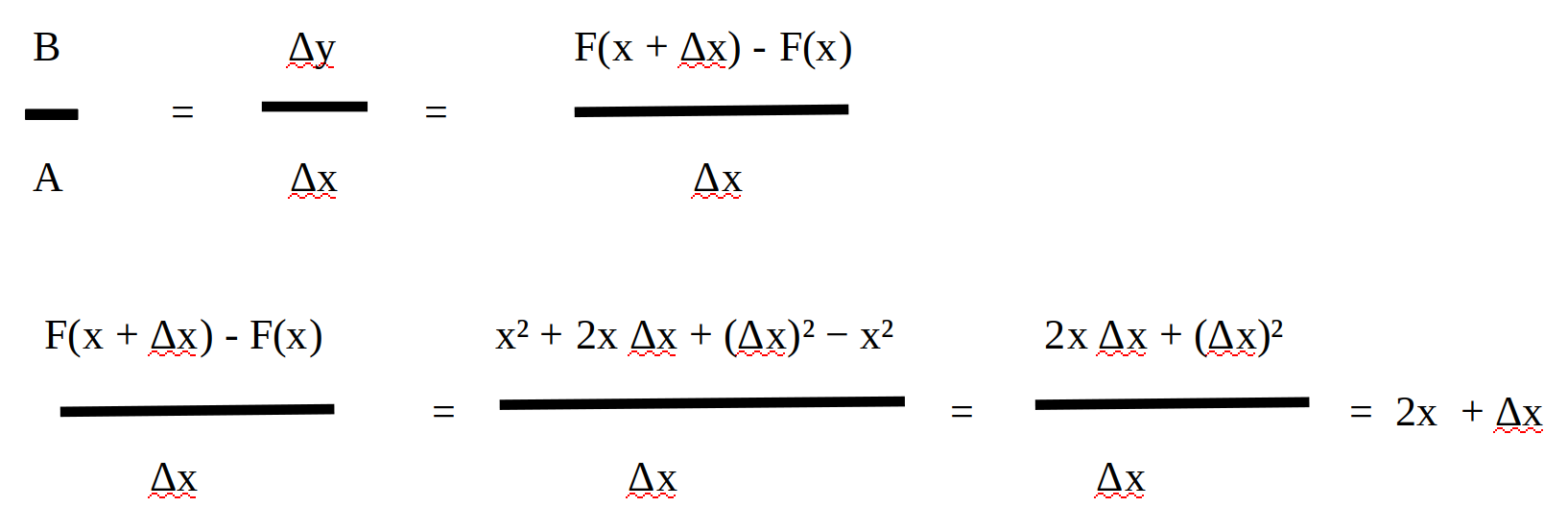
Et comme on part du principe que Δx = 0, alors on a 2x. Au point x, l’évolution, l’accélération, le coefficient directeur… est 2.
Karl Marx prend un autre exemple, avec une fonction plus complexe, cette fois non linéaire.
Il pose : F(x) = ax³ + bx² + cx – e = x’ ; cela implique qu’on connaisse a, b, c et e : Karl Marx utilise des lettres afin de généraliser.
Posons ensuite un y, avec F(y) = y’. On a alors :
x’ = ax³ + bx² + cx – e
y’ = ay³ + by² + cy – e
Rappelons ici qu’on cherche A et B, dénommés désormais Δx et Δy.

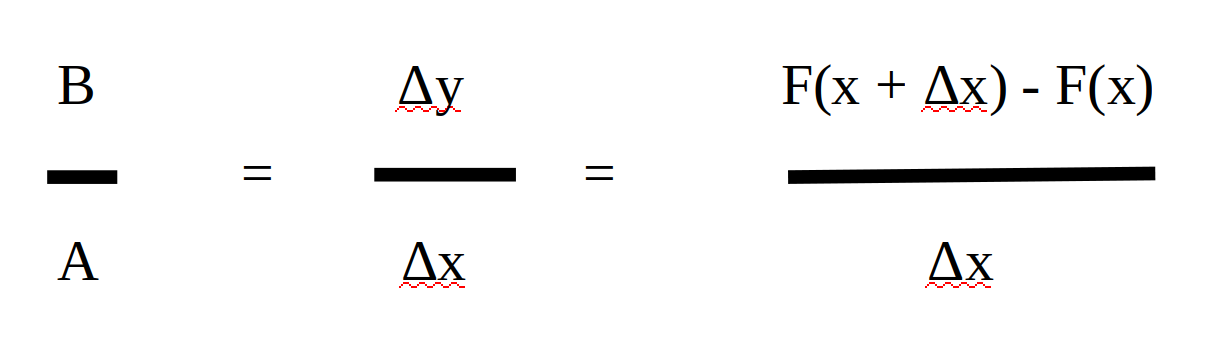
Ainsi, puisque :
x’ = ax³ + bx² + cx – e
y’ = ay³ + by² + cy – e
On a alors :
y’ – x’ = a (y³ – x³) + b (y² – x²) + c (y – x)
y’ – x’ = a (y – x) (y² + yx + x²) + b (y – x) (y + x) + c (y – x)
Et ainsi :

Et comme on part du principe pour la différentielle que x = y, alors cela donne:
a (x² + xx + x²) + b (x + x) + c = 3ax² + 2bx + c
On voit ici que, quel que soit x, on obtiendra forcément un résultat, même si x est égal à zéro.
Contrairement à l’exemple précédent, où on avait 2x, le rapport entre B et A est bien plus complexe.
On a ici un problème de fond.
On a réussi à trouver un résultat juste en un point, en utilisant la méthode de la dérivée, au moyen d’un Δx virtuel, c’est-à-dire d’une assimilation de x à un x’ virtuel.
Il y a ici une double problématique : tout d’abord, x est x’ et n’est pas x’.
On a ici un rapport dialectique, où les contraires sont identiques tout ne l’étant pas.
Ensuite, on a un calcul faux aboutissant à un résultat juste, puisque, à un moment on va se retrouver à diviser par 0, sauf qu’on ne le fait pas.
S’agit-il alors d’un vrai zéro, d’une quantité virtuelle ou d’une quantité réelle infime qu’on met de côté ?
Pour Karl Marx, ces deux aspects témoignent de la négation de la négation dans le processus. Il cherche alors à savoir d’où vient la transformation.
Il constate alors la chose suivante. Pour F(x) = ax, si :
F(x1) = ax1 = x2 et F(y1) = ay1 =y2
alors :
y2 – x2 = ay1 – ax1 = a(y1-x1)
soit :
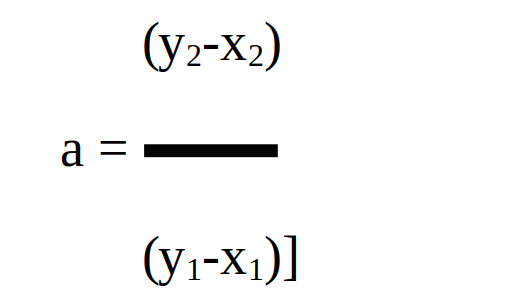
Il se demande alors d’où vient le mouvement dans le cadre d’une différentielle.
Si on prend y1, on s’aperçoit que ce nombre dépend de x1 (tout comme en fait y2 dépend de x2, mais la question ne se pose pas ici, car on a posé que x1 = x2).
On ne peut pas avoir par conséquent de mouvement indépendant des y : il faut se tourner vers les x.
C’est un aspect de la contradiction.
L’autre aspect, c’est que poser y1 = x1 implique a(y1-x1) = a(0) = 0
Autrement dit, pour qu’on ait un résultat, il faut une différence, mais pour obtenir cette différence, il faut un mouvement, qu’on supprime par définition en posant que x2 – x1 = 0.
Et on obtient pourtant tout de même un résultat, en mettant comme entre parenthèses cette négation.
Il n’y a alors qu’un seul moyen de s’en sortir, du point de vue de Karl Marx : considérer que l’opération est une négation de la négation.
Friedrich Engels, qui connaissait naturellement les manuscrits mathématiques de Karl Marx, résume cela ainsi dans son Anti-Dühring :
« Il en va de même en mathématiques.
Prenons une grandeur algébrique quelconque, par exemple a.
Nions-la, nous avons – a.
Nions cette négation en multipliant – a par – a, nous avons +a², c’est-à-dire la grandeur positive primitive, mais à un degré supérieur, à la seconde puissance.
Ici non plus, il n’importe pas que nous puissions obtenir le même a² en multipliant le a positif par lui-même pour parvenir aussi à a².
Car la négation niée est si ancrée dans a² qu’il a dans tous les cas deux racines carrées, soit a et -a.
Et cette impossibilité de se débarrasser de la négation niée, de la racine négative contenue dans le carré prend une signification très sensible dès les équations du second degré.
La négation de la négation apparaît d’une façon plus frappante encore dans l’analyse supérieure, dans ces additions “de grandeurs infiniment petites” que M. Dühring déclare lui-même être les opérations les plus élevées des mathématiques et que dans le langage ordinaire on appelle calcul différentiel et intégral.
Comment s’opèrent ces sortes de calculs ?
J’ai, par exemple, dans un problème déterminé deux grandeurs variables x et y dont l’une ne peut pas varier sans que l’autre varie aussi dans un rapport déterminé pour chaque cas.
Je différencie x et y, c’est-à-dire je suppose x et y si infiniment petits qu’ils disparaissent par rapport à n’importe quelle grandeur réelle si petite soit-elle, qu’il ne reste rien d’autre de x et de y que leur rapport réciproque, mais sans aucune base pour ainsi dire matérielle, un rapport quantitatif sans aucune quantité; dy/dx, le rapport des deux différentielles de x et y, est donc = 0/0, mais 0/0 posé comme expression de y/x.
Je ne mentionne qu’en passant le fait que ce rapport entre deux grandeurs disparues, l’instant de leur disparition promu à la fixité est une contradiction ; mais cela ne nous trouble pas plus que les mathématiques dans l’ensemble n’en ont été troublées depuis près de deux cents ans.
Qu’ai-je donc fait d’autre, sinon de nier x et y, mais non pas nier au point de ne plus m’en soucier, comme nie la métaphysique, mais nier de la manière correspondant au cas donné ?
Au lieu de x et y, j’ai donc leur négation dx et dy dans les formules ou équations qui sont devant moi.
Je continue dès lors à calculer avec ces formules, je traite dx et dy comme des grandeurs réelles bien que soumises à certaines lois d’exception, et arrivé à un certain point, je nie la négation, c’est-à-dire que j’intègre la formule différentielle, j’obtiens de nouveau à la place de dx et dy les grandeurs réelles x et y; mais je ne me retrouve pas disons aussi peu avancé qu’au début : j’ai au contraire résolu le problème sur lequel la géométrie et l’algèbre ordinaires se seraient peut-être cassé les dents. »
Seulement, cela ne résout pas la question de la transformation : où se déroule-t-elle ?
De fait, dès la parution de la traduction des Manuscrits mathématiques de Karl Marx par l’URSS révisionniste en 1968, la Chine populaire de la Grande Révolution Culturelle Prolétarienne s’est précipitée sur cette question, considérant qu’il y avait la clef pour de réelles mathématiques.
Il fallait étudier cette question de la différentielle pour comprendre comment les mathématiques pouvaient se développer en se conformant à la réalité matérielle en mouvement ; Friedrich Engels avait souligné dans La dialectique de la Nature que justement :
« Le calcul différentiel rend seulement possible à la science naturelle de présenter de manière mathématique non seulement des états, mais des processus : le mouvement. »
Les Manuscrits mathématiques en tant que tels seront traduits en chinois en 1975, mais dès 1968 leur questionnement de fond est connu et donne naissance à de nombreuses études qui vont s’élancer avec l’approfondissement de la Grande Révolution Culturelle Prolétarienne.
Cela produit un processus de refondation des études mathématiques, avec la publication en 1973 des trois volumes de « Mathématiques avancées » à destination des sciences réalisés en majeure partie par l’Université Fudan avec l’Université normale de Shanghai et l’Université des sciences et technologies de Shanghai, des deux volumes des « Mathématiques avancées » à destination des ingénieurs produits par l’Université de Tongji, de « Calcul » réalisé par l’École de génie chimique.
La question de la différentielle devient alors primordiale ; on a ainsi en 1974 une vague d’articles dans la Revue de la dialectique de la Nature, avec :
– « Comment comprendre le concept de limite ? » de He Fang,
– « La différentielle est comparable à zéro » de Zheng Li-Xing,
– « La différentielle est l’unité de zéro et de non-zéro » par Xu Ting-dong,
– « La différentielle reflète le changement quantitatif de (deux) différents points de vue » de Shen Tian-ji,
– « La différentielle est l’unité des opposés » de Ren Zheng-wing,
– « Sur l’expérience d’appliquer la dialectique à la réforme de l’apprentissage du calcul » de Fu Xi-tao…
Pour 1975, il faut mentionner :
– « Fonder le concept de dérivée sur la loi des opposés » de Yan Shao-zhong dans la Revue de l’université Fu Dan,
– « Comment comprendre les dérivées – notes en étudiant les manuscrits mathématiques de Marx » de Zhi Zhou dans la Revue de l’université normale de Pékin,
– « La brillante victoire de la dialectique – notes en étudiant les ‘‘manuscrits mathématiques’’ de Marx » de Zhejiang dans les Acta Mathematica Sinica,
– « La différentielle et la dialectique » par Wu Wen-jing dans la Revue de l’université Fu Dan,
– « Sur l’étude d’une lettre d’Engels pour une compréhension approfondie des Manuscrits mathématiques » de Zhu Xue-yan et Ou Yang Guang-zhong dans la Revue de l’université Fu Dan,
– « Comprendre le calcul du point de vue des paradoxes du mouvement » de Wu Wie-He dans le Bulletin scientifique,
– « Rapport préliminaire d’une conférence d’étude des ‘‘manuscrits mathématiques’’ de Marx » dans Pratique et compréhension des Mathématiques,
– « Utiliser le marxisme pour conquérir le champ de bataille des mathématiques » de Shu Li dans Science chinoise,
– « Un point de départ pour le calcul avec les différentielles » de Shu Zuo dans la Revue de l’université Fu Dan…
Pour 1976, il faut mentionner :
– « La différentielle est ‘‘l’infiniment petit’’ » de Zhou Guan-Xiong dans la Revue de l’université industrielle de Chine centrale,
– « Utiliser le point de vue du développement et de la transformation pour comprendre le calcul » par Wu Xie-He et Zhang Hua-xia dans la Revue du collège politique de Chine centrale,
– « La différentielle est l’unité des opposés (synthèse des antithèses) zéro et non-zéro » de Yu Wen dans la Revue de l’université industrielle de Chine centrale,
– le « Résumé des discussions du symposium d’étude des ‘‘manuscrits mathématiques’’ de Marx » de Quao Chong-qi dans Pratique et compréhension des Mathématiques,
– « Un brillant exemple utilisant le matérialisme dialectique pour transformer les mathématiques » de Huang Shun-ji dans la Revue de l’université normale de Pékin,
– « La différentielle est l’anti-thèse / la synthèse de zéro et de l’infiniment petit » de Gao Ke-qiang dans la Revue de l’université industrielle de Chine centrale,
– « L’étude des visions différentes du monde à partir de deux approches différentes des mathématiques » par le groupe d’étude des Manuscrits mathématiques de Marx du département de mathématiques de l’école normale des enseignants dans Pratique et compréhension des Mathématiques…
Les apports de la Grande Révolution Culturelle Prolétarienne permettent de comprendre la question de la différentielle.
Le fond du problème est la question du repère cartésien.
Ce repère divise comme on le sait graphiquement les abscisses des ordonnées , mais son arrière-plan est de diviser l’espace et le temps.
Si on prend le graphique initial avec le parcours d’un cycliste en dix secondes, on voit bien la séparation.

Cette séparation révèle son caractère arbitraire si on prend le repère en partant des trois cas de figures.
En effet, soit on connaît le temps mais pas la distance parcourue (c’est la thèse), soit on connaît cette dernière mais pas le temps effectué (c’est l’antithèse)…
Soit on connaît les deux ou ni l’un ni l’autre (c’est la synthèse).
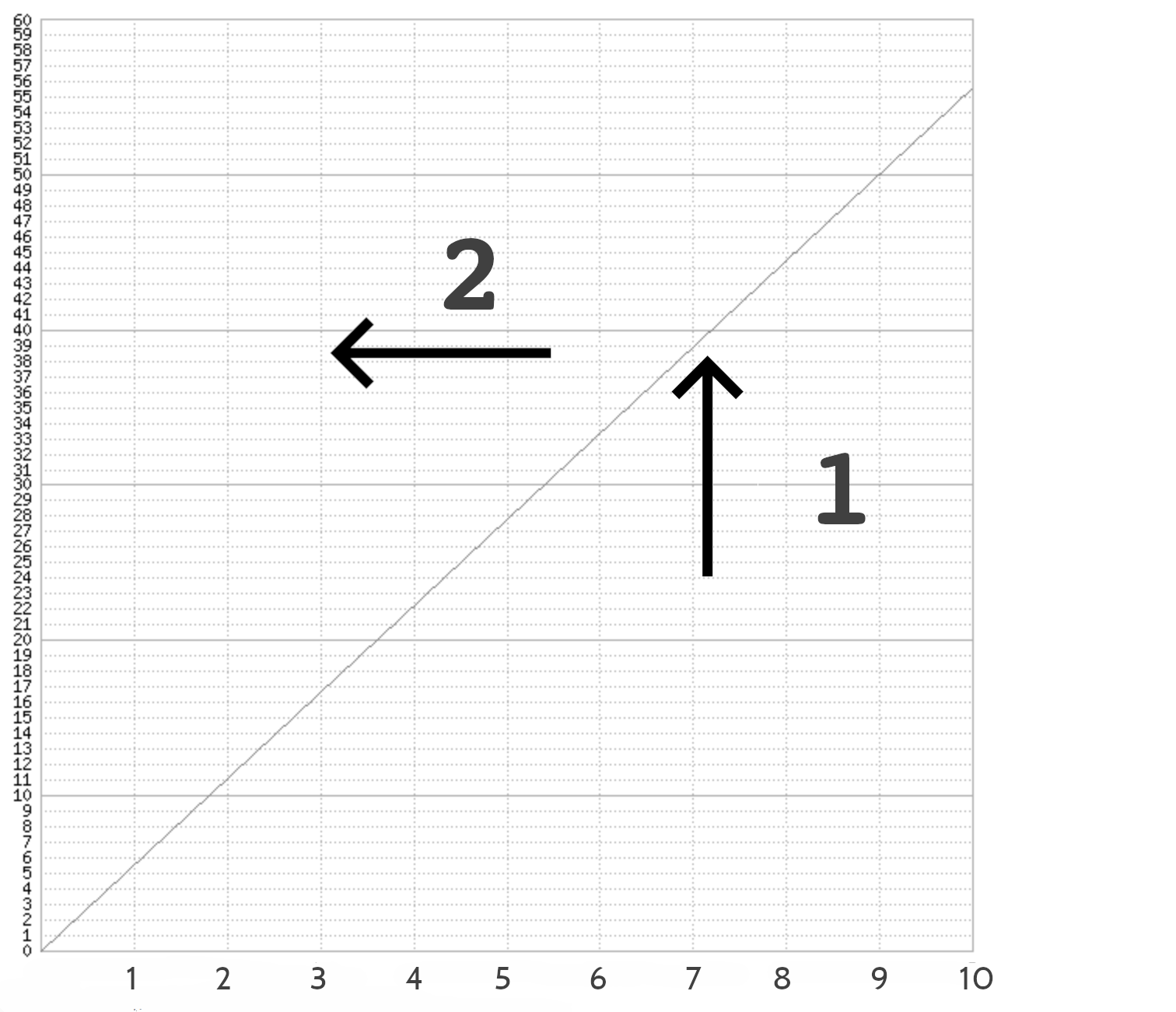
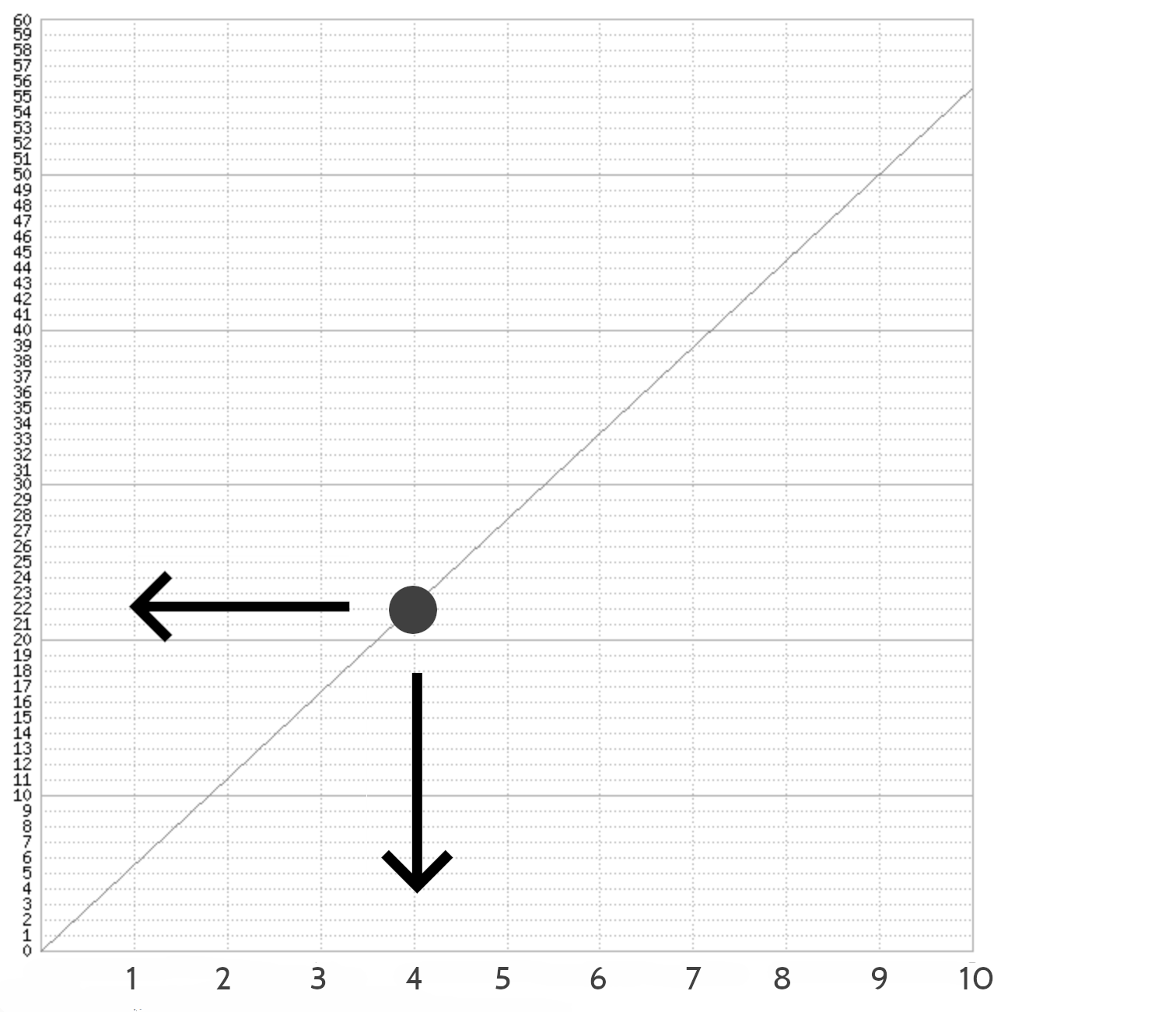
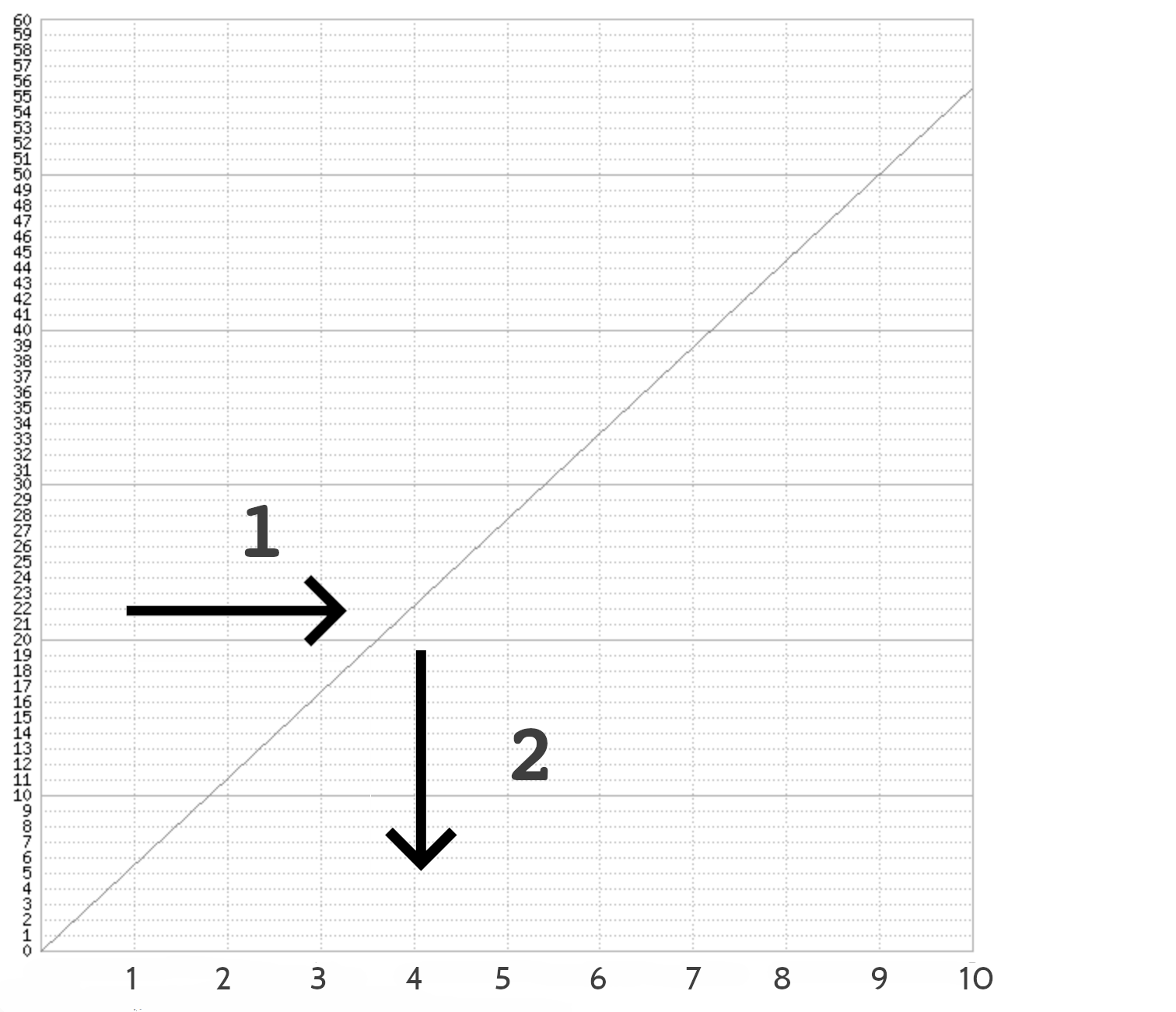
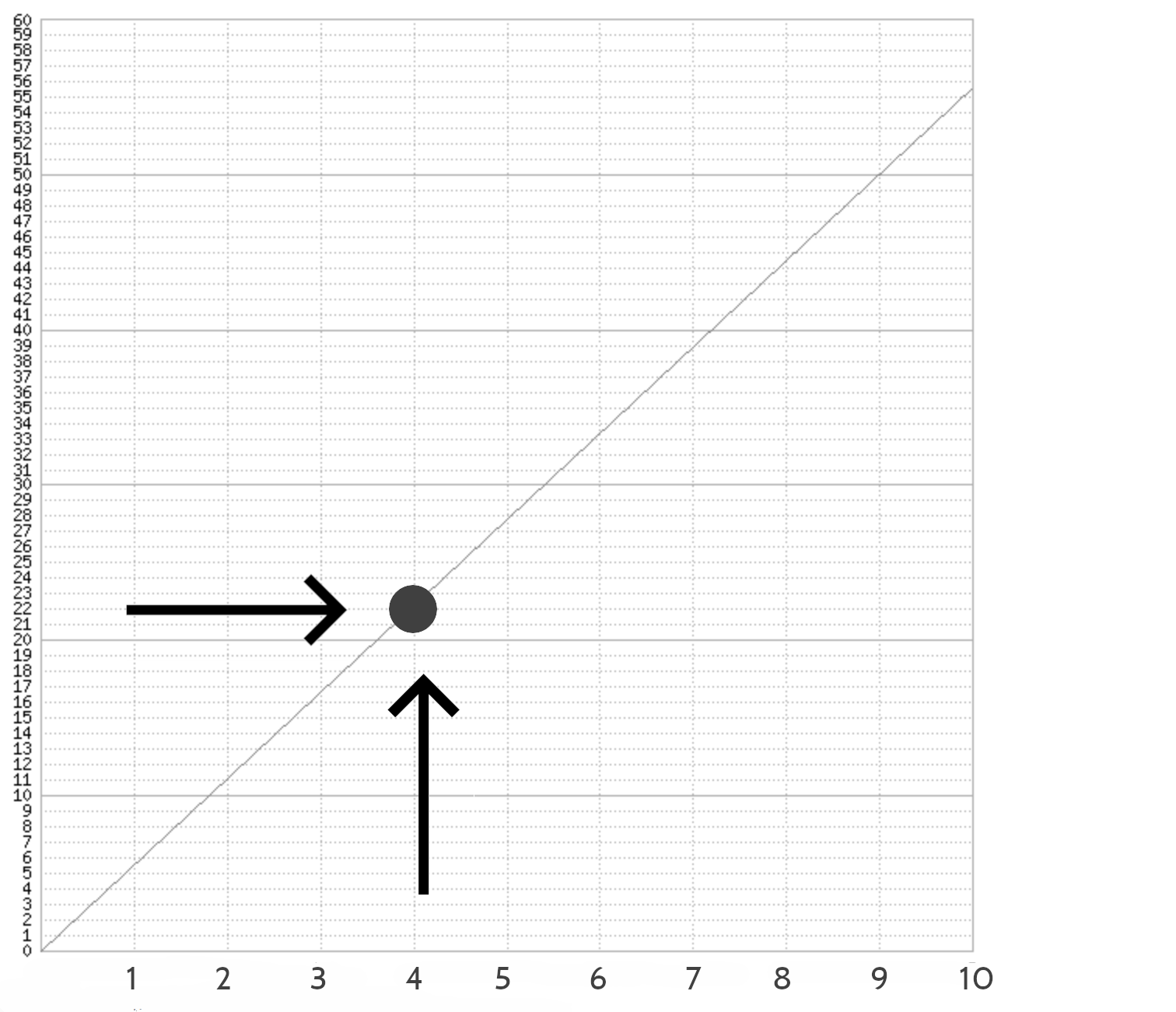
Or, de ces représentations, il n’y a que la synthèse qui corresponde à la réalité.
En effet, ce qui est représenté est en mouvement.
Et pourtant, lorsqu’on prend la thèse ou l’antithèse, lorsqu’on prend le temps effectué ou la distance parcourue, on supprime le mouvement puisqu’on abandonne le point concerné pour se diriger vers l’information manquante.
Autrement dit, lorsqu’on dispose du temps effectué, qu’on se tourne vers le point concerné pour connaître l’équivalent en termes de distance parcourue, comme dans le schéma suivant, on passe du temps à l’espace par l’intermédiaire du point – alors que le point est ce qui justifie tant l’espace que le temps.

Ce n’est pas tout.
On a ici un mouvement linéaire, mais dans le cas où il n’y a pas de linéarité, la représentation échoue à la représenter figurée.
On comprend également cette idée lorsqu’on s’intéresse au jeu d’échecs. Ici, le mouvement possible de la tour qui est linéaire non évolutif correspond dans les faits au repère cartésien, le mouvement possible du fou à un mouvement linéaire évolutif, le mouvement possible du cavalier à un mouvement non linéaire.

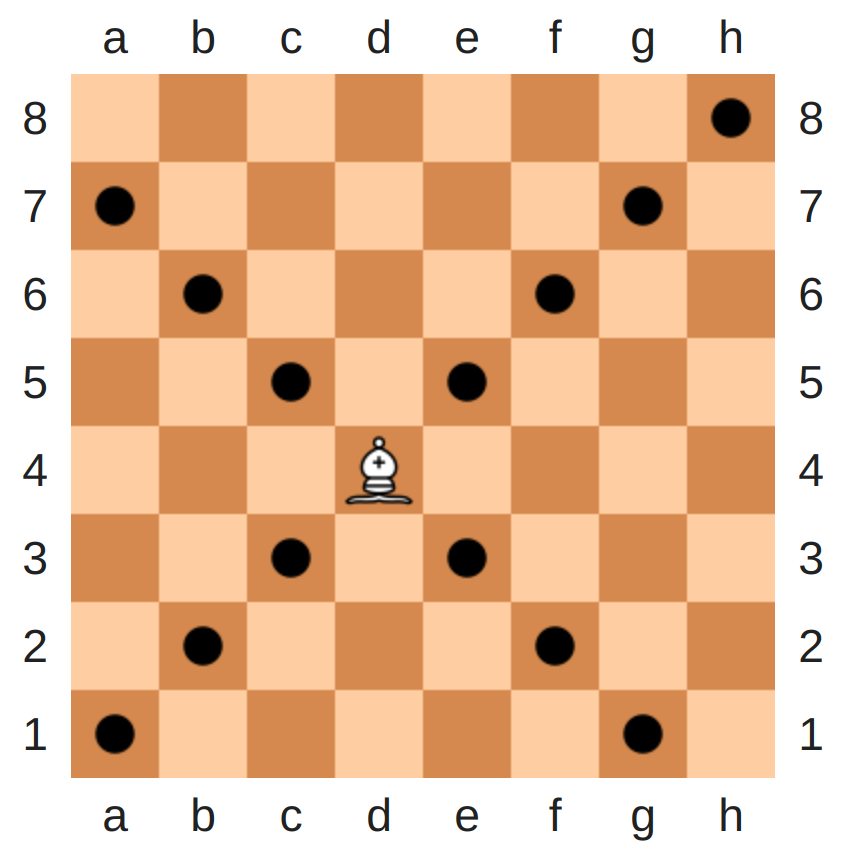
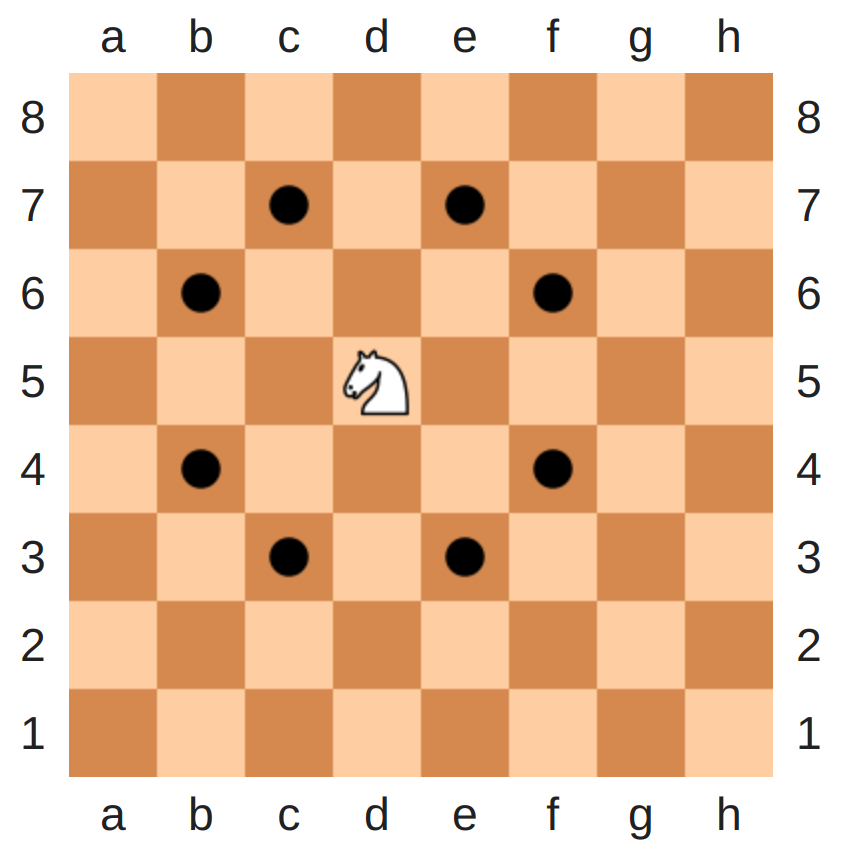
Or, le mouvement du cavalier combine dans les faits le mouvement de la tour et celui du fou. Qui joue aux échecs sait que cela pose un problème fondamental. Et cela revient très exactement à :
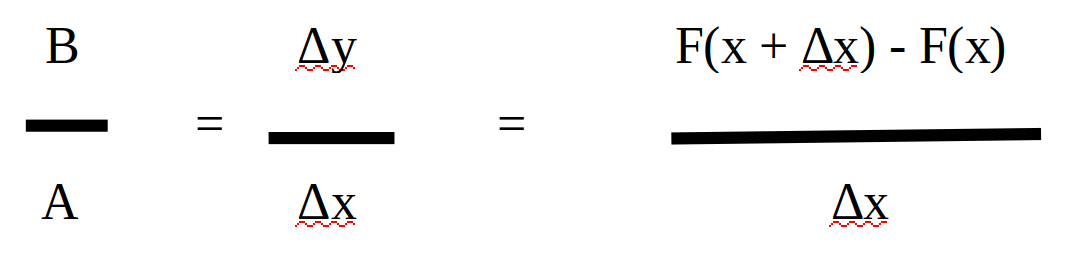
Le mouvement qui se réalise tend en effet à s’autosupprimer en se réalisant.
C’est cela qui oblige à ce qu’on trouve un élément qui soit 0 et non 0 en même temps.
Pour Karl Marx, Δx = 0 et revient à une négation, qui va connaître une négation pour qu’on parvienne au résultat.
Cependant, le résultat est là en même temps que la première négation, car si dans le calcul on a un processus, le calcul fige le processus.
C’est pourquoi Mao Zedong dit qu’il n’y a pas de négation de la négation, que parler de l’unité des contraires suffit.
Autrement dit, et là est le piège dans la différentielle : la fonction indique une évolution.
Cette évolution est représentée graphiquement. Cependant, chaque point n’existe en réalité pas en même temps avec les autres, il y a succession, l’un devenant l’autre.
On peut faire un tableau avec les mètres et les secondes. Mais ce tableau est faux.
| 1 | 5,56 |
| 2 | 11,12 |
| 3 | 16,68 |
| 4 | 22,24 |
| 5 | 27,80 |
| 6 | 33,36 |
| 7 | 38,92 |
| 8 | 44,48 |
| 9 | 50,04 |
| 10 | 55,60 |
Il faudrait avoir initialement cela.
| 1 | 5,56 |
Puis ensuite cela.
| 2 | 11,12 |
Et ainsi de suite.
Il faudrait même diviser à l’infini, ne pas en rester aux secondes ni aux mètres, car les secondes sont divisibles à l’infini, tout comme les mètres – ce qui aboutirait à des tableaux à l’infini, et ramène aux problématiques du mouvement posées dans l’antiquité par Zénon d’Élée et auxquelles seul le matérialisme dialectique peut répondre.
Car c’est le mouvement de la matière, par la matière elle-même, qui établit l’espace, le temps étant une expression de ce mouvement dans l’espace, ou plus exactement de ce mouvement de l’espace dans lui-même par lui-même.
La différentielle est en fait le point où les mathématiques, comme connaissance prenant appui sur elle-même, connaît un saut dialectique dans sa propre avancée, et cela parce que le principe de la fonction correspond à la contradiction entre l’espace et le temps, par le mouvement.
C’est pour cela que Friedrich Engels dit que du moment où l’on sépare l’espace et le temps dans un repère cartésien, alors on tombe sur la différentielle inévitablement – les travaux de Leibniz et de Newton sur la différentielle étaient inévitables de par le cadre posé, au-delà de leurs méthodes différentes.
La notion de 0 qui n’est pas 0 correspond au déplacement d’une chose, qui est et n’est pas à sa place, et en fait c’est vrai de tout phénomène tout le temps, car tout est en mouvement.
Ce qui se passe dans la différentielle, ce n’est pas qu’on utilise un y virtuel infiniment proche de x, c’est qu’en réalité ce y est x et n’est pas x – conformément à la nature dialectique de x.
La différentielle est le moment où les mathématiques découvrent que le calcul est l’unité des opposés de la division infinie et de l’agrégation infinie, comme cela a été compris lors de la Grande Révolution Culturelle Prolétarienne.
C’est parce qu’il avait compris que la différentielle reposait sur cette question de la division et de l’agrégation que Friedrich Engels disait justement dans La dialectique de la Nature :
« La chimie décompose les molécules en atomes, grandeurs d’une masse et d’une extension spatiale plus faibles, mais grandeurs du même ordre, de sorte que les unes et les autres sont réciproquement dans des relations finies déterminées.
L’ensemble des équations chimiques qui expriment la composition moléculaire des corps sont donc par leur forme des équations différentielles.
Mais, en réalité, elles sont déjà intégrées du fait des poids atomiques qui y figurent.
C’est avec des différentielles, dont le rapport réciproque de grandeur est connu, que la chimie calcule. »