Prenons un exemple de conversion avec CAmEstrEs, réduit à CelArEnt. La base de CamEstrEs est la suivante :
Tout A est B, or aucun C n’est B, donc aucun C n’est A.
Ce qui donne, par exemple :
Tout rat est un rongeur, or aucun cheval n’est un rongeur, donc aucun cheval n’est un rat.
CelArEnt est un syllogisme du type :
Aucun A n’est B, or tout C est A, donc aucun C n’est B.
Par exemple :
Aucun contre-révolutionnaire n’est un révolutionnaire,
Or tout bourgeois est un contre-révolutionnaire,
Donc aucun bourgeois n’est un révolutionnaire
Pour prouver véritablement CamEstrEs, il faut le « réduire » à CelArEnt, car en fait CamEstrEs revient à CelArEnt.
Voici comment, dans les premiers analytiques, Aristote explique cette conversion :
« Si M est à tout N, et n’est à aucun O, O ne sera non plus à aucun N.
Car si M n’est à aucun O, O non plus ne sera à aucun M; mais M était supposé à tout N, donc O ne sera à aucun N ; ainsi on est revenu à la première figure. Mais, comme la proposition négative se convertit, N ne sera non plus à aucun O, et alors le syllogisme sera le même.
On pourrait démontrer encore ceci par réduction à l’absurde. Il est donc évident que, les termes ainsi disposés, il y a syllogisme, mais non pas syllogisme complet ; car la conclusion nécessaire ne se forme pas uniquement avec les données primitives ; il faut, en outre, d’autres éléments. »
Traduisons cela. Cela donne :
M est à tout N
M n’est à aucun O
donc O
n’est à aucun N
[reprise de la seconde affirmation] M n’est à aucun O
[conversion, en inversant] O n’est à aucun M
[reprise de la première affirmation] M est à tout N
[arrivée à CelArEnt] donc O n’est à aucun N.
[conversion de la négative] aucun N n’est à O
Quelle est la différence ? Dans la première édition de l’Encyclopédie, en 1751, on s’en moquait et on parlait des « galimatias de l’école sur les réductions des syllogismes ».
L’article sur les réductions explique également que les modifications pour retrouver les syllogismes parfaits à partir de ceux imparfaits consistent en « des changements dont la recherche ne suppose pas peut-être moins d’esprit que les plus sublimes démonstrations géométriques ».
C’est effectivement peu pratique, mais l’idée est somme toute la suivante. Prenons un exemple concret, en se fondant sur la forme des syllogismes.
CamEstrEs est du type suivant, avec un exemple :
Tout A est B, or aucun C n’est B, donc aucun C n’est A.
Tout arbre est un végétal, or aucun rat n’est un végétal, donc aucun rat n’est un arbre.
CelArEnt est du type suivant, avec un exemple :
Aucun A n’est B, or tout C est A, donc aucun C n’est B.
Aucun animal n’est végétal, or tout rat est animal, donc aucun rat n’est un végétal.
La différence est ici flagrante. On monte d’un cran dans la connaissance.
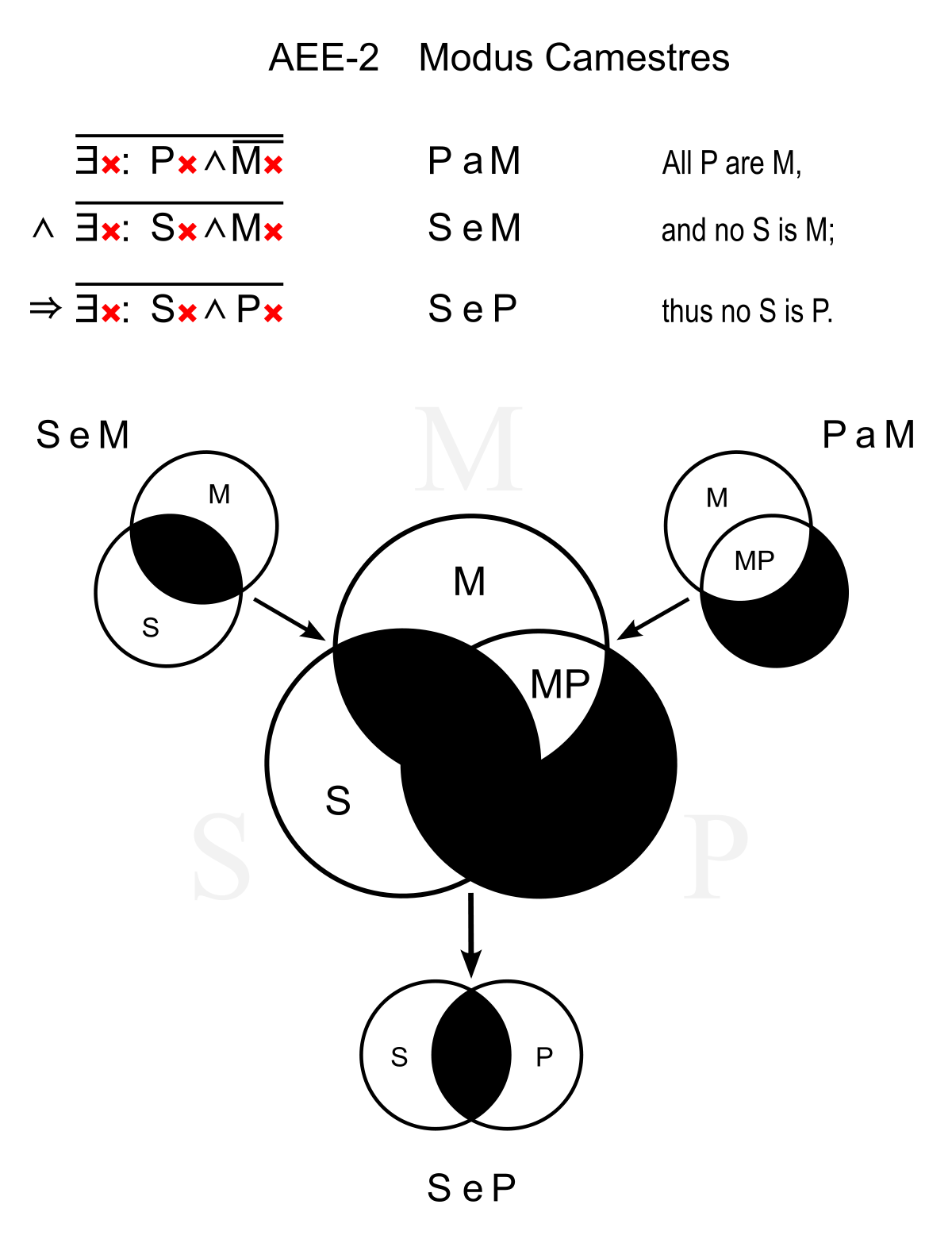
Pour bien saisir cela, regardons des graphiques : ceux de CamEstrEs et CelArEnt. Rappelons leur contenu, en utilisant les mêmes lettres que dans le graphique pour mieux comprendre.
Tout P est M or aucun S n’est M, donc aucun S n’est P
Aucun M n’est P, or tout S est M, donc aucun S n’est P.
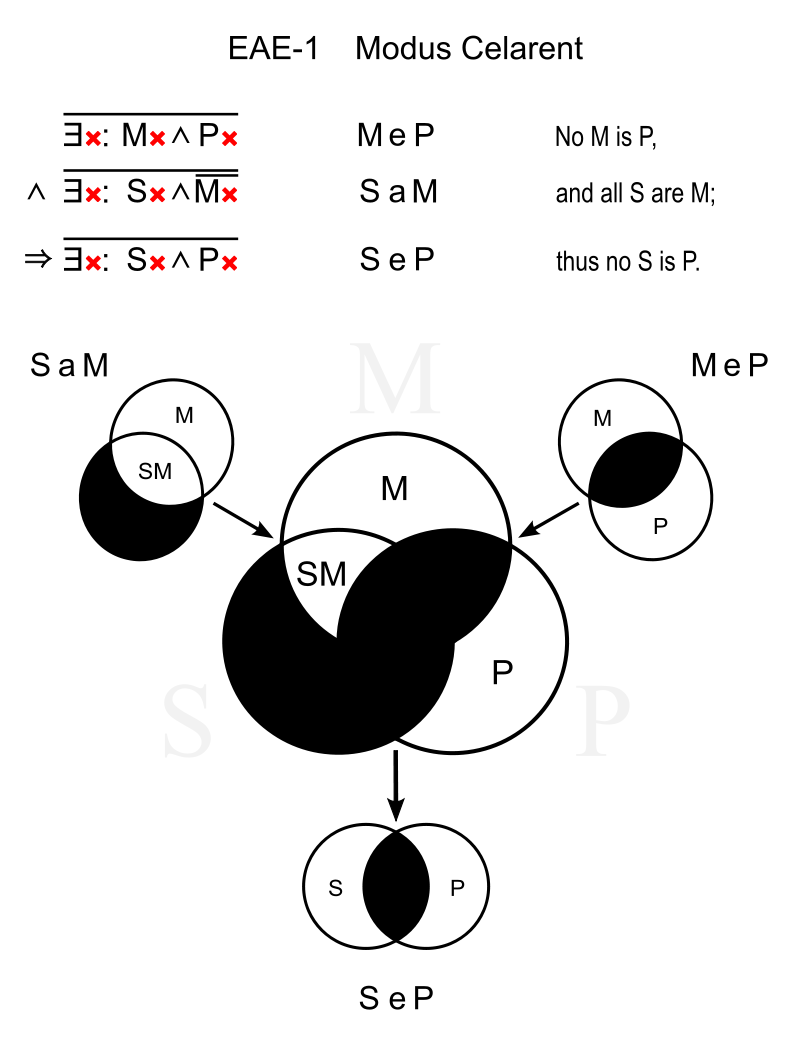
Quel est le but ? De parler de S. Or, dans la première figure, S est définie négativement. Alors que dans la seconde S fait partie d’un ensemble, il est défini positivement.
C’est très clairement une approche casse-tête, mais qui vise à cerner la notion d’identité (positive et contradictoire par rapport à d’autres, et pas simplement négative), d’universel et de particulier.
C’est une sorte d’énorme contournement du matérialisme dialectique.
Comme c’est justement une forme à la fois contournée et ancienne dans le développement de la pensée, elle est justement malaisée à saisir.