Il est bien connu que le triangle équilatéral est un symbole de l’idéalisme, étant associé à l’harmonie et l’éternité. On le trouve dans la forme des pyramides égyptiennes, dans l’étoile de David, le symbole de Dieu dans les églises, comme symbole du grand architecte de la franc-maçonnerie, etc.
Au-delà de cette utilisation mystico-religieuse, il y a lieu de se poser la question de savoir pourquoi le triangle a été conceptualisé par l’humanité. On ne le retrouve en effet pas dans la Nature et c’est pour cela d’ailleurs qu’il est un symbole idéaliste de la supériorité divine.
Pour parvenir à la notion de triangle, comment a procédé l’humanité ? C’est une tentative délicate que de reconstruire le cheminement effectué, mais on peut discerner quelques bases essentielles.
La base du triangle, c’est en effet la ligne droite. Pour parvenir à la forme du triangle, il faut déjà tracer une ligne droite, puis il en faut deux autres. On trouve alors deux aspects.
Le premier aspect, c’est la pratique. Dans la vie quotidienne, l’humanité ne comprenant pas la dialectique raisonne de manière unilatérale. Quand on mange une soupe, la soupe est mangée : il y a une ligne droite d’une étape à l’autre, ou si l’on veut une cause et conséquence. Il y a un résultat final, qui suit un point de départ, une origine.
Lorsqu’on se déplace de Rome à Athènes, on a réalisé quelque chose, on a suivi une ligne droite, puisque le résultat est le déplacement. Peu importe que le chemin réel n’ait pas été en ligne droite, qu’il y ait une série de contradictions dans le mouvement, etc. : l’humanité raisonnant de manière unilatérale voit un début et une fin.
L’exemple le plus connu de cette lecture unilatérale des choses, c’est « Dieu dit : que la lumière soit. Et la lumière fut ».
Cette notion de ligne droite est ainsi le produit de l’activité humaine. Les animaux ne peuvent pas conceptualiser cette notion de ligne droite, car leurs activités ne transforment pas leur environnement comme le fait l’être humain ; les animaux vivent la dialectique de manière immédiate, alors que l’humanité transformatrice fétichise son résultat de grande ampleur (au sens de grande pour lui, car non naturelle).
La pratique humaine a donc amené la systématisation de la notion de ligne droite. Une systématisation de ce type a abouti à sa fétichisation.
Le second aspect, c’est la théorie. Imaginons une ligne droite et chercherons à la faire se rejoindre elle-même. C’est impossible.
Si on a un cercle, on peut prendre un point et revenir à lui, en suivant simplement le cercle. Une ligne droite implique deux sens opposés et il n’y a pas de « retour ».
On peut bien ajouter une autre ligne droite pour impliquer un mouvement extérieur, mais alors on ne rejoint toujours pas la ligne droite initiale.
Par contre, si on ajoute une troisième ligne droite, alors on obtient un « retour » à la ligne droite. On part d’une ligne droite, on utilise une autre ligne droite qui amène à une troisième ligne droite ramenant à la première.
△
Seulement, le triangle équilatéral devient alors essentiel, car en accordant la même longueur aux trois côtés, aucun ne prime sur l’autre. On peut donc dire qu’on revient toujours à la ligne droite en général, quelle que soit la ligne droite qu’on prenne. Sans cela, on reviendrait à une ligne droite en particulier.
Le triangle (équilatéral) est donc le fétichisme de la ligne droite.
Pourquoi toutefois se fonder sur le triangle, plutôt que sur le carré ou le cercle ?
Ici on peut se tourner vers le « Tetraktys » de Pythagore, qui a vécu en Grèce antique au 6e siècle avant notre ère. Pythagore avait élaboré toute une mystique des nombres, qui ne nous intéresse pas ici. Ce qui compte, c’est qu’il valorise 1 + 2 + 3 + 4 = 10 comme clef pour comprendre le monde, et que dans la forme dite « Tetraktys » qu’il propose pour présenter cette clef, on retrouve le triangle.
Chaque élément étant à équidistance des autres, on peut en effet établir une série de triangles.
La tradition pythagoricienne associe le 1 au point, le 2 à la ligne, le 3 à la surface. Et effectivement, le moyen le plus court d’établir une surface est d’employer un triangle. On raisonne aujourd’hui en termes de carré, par exemple avec les m². Cependant, un carré, c’est deux triangles. Pour arriver au carré, on passe en fait par le triangle.
Le triangle précède le carré ; on a un exemple intéressant du rapport entre triangle et carré dans le théorème de Pythagore justement, qui dit que dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Dans l’image suivante, l’aire du grand carré bleu est la somme des aires des deux autres carrés.
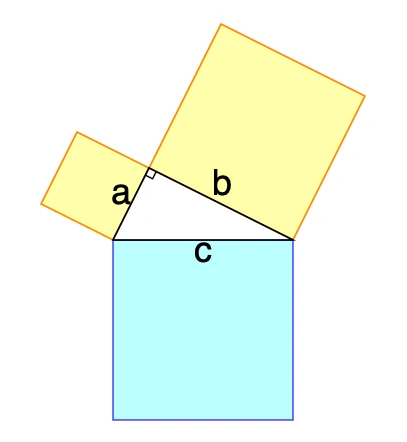
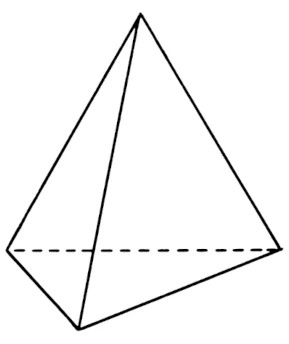
En fait, utiliser un triangle puis un autre triangle équivalent revient également à en utiliser deux similaires, ce qui donne un carré ou un rectangle. Et c’est important de voir que le triangle précède, car arriver à quatre côtés, c’est établir un volume, et non plus simplement une surface. Le tétraèdre est un triangle mais avec un volume, de par ses quatre côtés.
La tradition pythagoricienne connaît pour cette raison une prière à ces 1, 2, 3, 4 rassemblés en la figure « Tetraktys », qui « contiendrait » toutes les dimensions :
« Bénis-nous, nombre divin, toi qui as engendré les dieux et les hommes ! Ô sainte, sainte Tétractys, toi qui contient la racine et la source de la création qui coule éternellement !
Car le nombre divin commence par l’unité profonde et pure jusqu’au saint quatre ; puis il engendre la mère de tous, le tout-comprenant, tout-liant, le premier-né, le saint dix inébranlable, infatigable, le détenteur de la clé de tous. »
On comprend alors ici très bien la genèse du triangle. En fait, l’humanité a découvert la ligne droite en considérant de manière unilatérale le résultat de sa propre activité. L’association d’une ligne droite à une autre aboutit à l’utilisation d’une troisième pour revenir à une ligne droite qui ne cesse jamais.
Les lignes droites d’un triangle sont ainsi l’équivalent d’un cercle. Un cercle circonscrit une surface et si on prend un point d’un cercle et qu’on continue sur le cercle, on y retourne. On a la même chose avec le triangle, à la différence qu’avec ce « cercle » on conserve la ligne droite.
Et à la différence du cercle, le triangle permet aisément le calcul des surfaces. Le triangle a été fétichisé comme réalisation de la ligne droite, comme reflet de l’approche unilatérale et par son utilisation concrète comme base de calcul des surfaces.
>>Revenir au sommaire des articles sur le matérialisme dialectique