
des peuples de l’URSS !
Les mathématiques posent le principe de la division comme un moyen de trouver aisément une équivalence. Prenons par exemple :
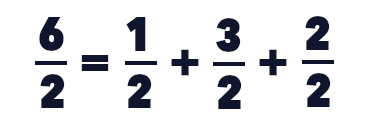
Les mathématiques disent qu’il est d’abord possible de rassembler les numérateurs de la partie droite puisqu’ils ont le même dénominateur. Cela donne :
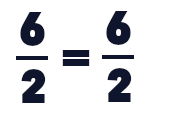
Puis, les mathématiques disent que puisque de toutes façons le dénominateur est le même, alors on peut s’en passer.

Il n’y a ici rien d’étonnant, rien de choquant. Pourtant, il y a ici toute une série de raccourcis qui posent un véritable problème théorique.
En effet, au sens strict, dire que :

parce que :
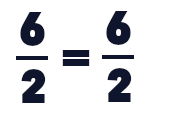
cela implique logiquement de dire que :
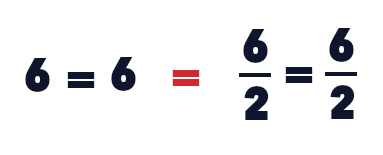
Or, le souci est que :
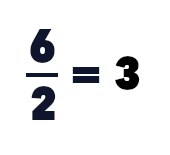
Ce qui ramène alors au fait erroné mathématiquement parlant comme quoi :
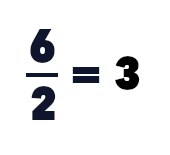
Le nœud du problème est que lorsqu’on pose :
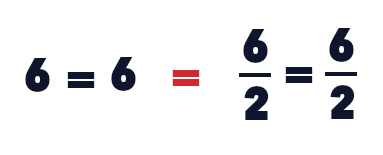
on doit plus précisément entendre :
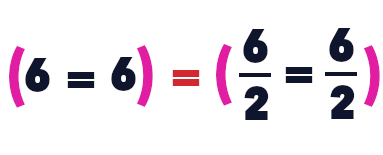
Cela ne change cependant rien à l’affaire ou, plus exactement, cette affaire est dialectique. Il y a ici un phénomène dialectique qui n’est pas apparent.
Il faut en effet bien que 6 = 6, puisque c’est une question d’identité. 6 n’est en même temps pas seulement 6, car il peut devenir 3. Il est dialectiquement 6 et non 6. En ce sens, on a bien 6 = 3 puisque sinon 6 ne pourrait jamais devenir 3. Et il le devient par la division par 2, qu’on peut utiliser ou non.
Karl Marx aurait ici parlé de négation de la négation. En additionnant, à droite de l’opération initiale, les numérateurs 1, 3 et 2, on procède à une négation des numérateurs. Et en supprimant ensuite le dénominateur 2 des deux côtés, on procède à la négation de la négation, car la division par 2 est devenue la négation fondamentale découlant de l’addition des numérateurs !
Voici ce que cela donne schématiquement.
On a l’opération initiale.
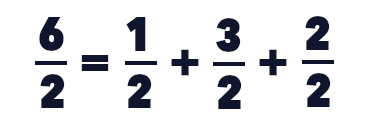
On additionne les numérateurs à droite : on les nie en les rassemblant. Cela donne :
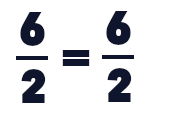
On procède alors à la négation de la négation. Mais la négation n’est plus dans les numérateurs désormais, elle est dans le dénominateur. La négation s’est retournée en son contraire ! C’est donc la division qui est la négation, qu’il s’agit de supprimer. Ce qui donne :

Mais comme Mao Zedong a raison, il faut considérer que la négation de la négation existe bien, mais n’est pas une proposition absolue car tout est relié à tout, et on s’aperçoit de l’importance du fait que dans le processus de négation de la négation, on ait :
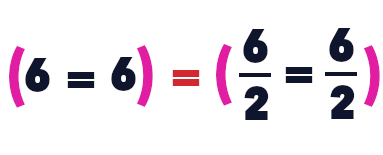
Cela ramène en effet à :
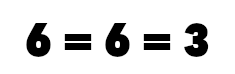
C’est là qu’on comprend l’apport de Mao Zedong, puisque si on suit uniquement la négation de la négation on obtient une identité unilatérale, 6 = 6, alors que si on voit la dialectique à tous les niveaux, on constate qu’il y a 6 = 3 qui découle du processus.
C’est là une limite à la forme mathématique, car mathématiquement 6 n’est pas égal à 3, mais 6 peut pourtant bien se ramener à 3 dans un processus de transformation. La négation de la négation ne se pose pas de manière découplée du reste, elle relève d’une vague (forcément infinie et éternelle de par ses liaisons dialectiques infinies).
L’équivalence utilisée dans la division, avec la question du dénominateur qu’on peut mettre de côté ou non, est vue comme un raccourci mathématique pratique ; elle reflète en réalité une réalité dialectique, celle d’une avancée vers un résultat impliquant une remise en cause de l’identité du nombre – 6 devenant ici 3 – comme témoignage du mouvement inexorable de chaque chose dans ses liaisons inépuisables au niveau de l’univers.
>>Revenir au sommaire des articles sur le matérialisme dialectique